Frequency/Harmonic Response
This solution is included with NX NASTRAN Dynamic Response
Dynamic Response in Nastran
Dynamic Frequency Response in Femap
Overview
In NX Nastran, use:
- SOL 108 to perform direct frequency response analysis.
- SOL 111 to perform modal frequency response analysis.
The direct frequency response method solves the coupled equations of motion in terms of forcing frequency. The modal frequency response method utilizes the mode shapes of the structure to:
- Reduce the problem size because not all of the modes are typically calculated or retained.
- Uncouple the equations of motion when either no damping or only modal damping is used.
The solution at a particular forcing frequency is obtained through the summation of the individual modal responses. Phase Shift Oscillatory loading is sinusoidal in nature. In its simplest case, this loading is defined as having an amplitude at a specific frequency. The steady-state oscillatory response occurs at the same frequency as the loading. The response may be shifted in time due to damping in the system. The shift in response is called a phase shift because the peak loading and peak response no longer occur at the same time. An example of phase shift is shown in Figure 6-1.
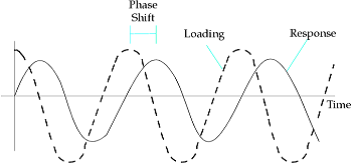
Figure 6-1. Phase Shift
Complex Numbers The important results obtained from a frequency response analysis usually include the displacements, velocities, and accelerations of grid points as well as the forces and stresses of elements. The computed responses are complex numbers defined as magnitude and phase (with respect to the applied force) or as real and imaginary components, which are vector components of the response in the real/imaginary plane. These quantities are graphically presented in Figure 6-2.
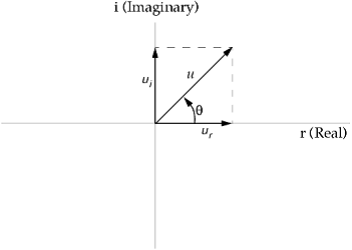
Figure 6-2. Phase Shift
where: u = Magnitude = q = Phase angle = tan-1 (ui/ur) ur = Real component = u cos q ui = Imaginary component = u sin q Direct Frequency Response Analysis (SOL 108) In direct frequency response analysis, structural response is computed at discrete excitation frequencies by solving a set of coupled matrix equations using complex algebra. Modal Frequency Response Analysis (SOL 111) Modal frequency response analysis is an alternate method to compute frequency response. This method uses the mode shapes of the structure to uncouple the equations of motion (when no damping or only modal damping is used) and, depending on the number of modes computed and retained, reduce the problem size. Both of these factors tend to make modal frequency response analysis computationally more efficient than direct frequency response analysis. Because modal frequency response analysis uses the mode shapes of a structure, modal frequency response analysis is a natural extension of normal modes analysis.


